1. Introduction
LU 분해(Factorization)는 정사각 행렬 A 를 두 개의 행렬 L (Lower triangular matrix)과 U (Upper triangular matrix)의 곱으로 표현하는 기법이다. 즉,
A = LU
이 성립한다. 이를 활용하면 선형 방정식 풀이, 행렬식 계산, 역행렬 구하기 등의 연산을 효율적으로 수행할 수 있다.
2. LU Factorization Process
LU 분해 과정은 아래와 같다.
- 행렬 A를 설정한다.
import numpy as np
A = np.array([[2, 3, 1],
[4, 7, 3],
[-2, 3, 4]])
print("A =\n", A)
- 행 연산을 통해 A를 삼각 행렬로 변환한다.
- 첫 번째 열을 기준으로 가우스 소거법을 수행하여 U 행렬을 얻는다.
- 이때, 수행한 연산을 기록하여 L 행렬을 생성한다.
- 결과적으로 아래와 같은 형태의 LU 분해를 얻는다.
from scipy.linalg import lu
P, L, U = lu(A)
print("L =\n", L)
print("U =\n", U)
이때, L 행렬은 단위 하삼각행렬(lower triangular matrix with ones on the diagonal), U 행렬은 상삼각행렬(upper triangular matrix)이다.
3. Application of LU Factorization
LU 분해는 다양한 응용이 가능하다.
- 선형 방정식 풀이:
- 주어진 방정식 Ax = b 에 대해, 먼저 Ly = b 를 풀고, 이후 Ux = y 를 푼다.
b = np.array([5, 9, 4])
y = np.linalg.solve(L, b)
x = np.linalg.solve(U, y)
print("Solution x =", x)
- 행렬식 계산:
- A = LU 일 때, det(A) = det(L) * det(U) 가 성립하며, L 의 대각 원소가 1이므로 det(A) = det(U) 로 쉽게 계산할 수 있다.
det_A = np.linalg.det(U)
print("det(A) =", det_A)
- 역행렬 계산:
- A^{-1} = U^{-1} * L^{-1} 를 이용하여 역행렬을 구할 수 있다.
A_inv = np.linalg.inv(U) @ np.linalg.inv(L)
print("A_inv =\n", A_inv)
4. Summary
LU 분해는 정사각 행렬을 하삼각행렬과 상삼각행렬의 곱으로 분해하는 기법으로, 선형 시스템 해법, 행렬식 계산, 역행렬 구하기 등 다양한 응용이 가능하다. 특히 계산을 효율적으로 수행할 수 있어 수치해석에서 중요한 개념이다.
# LU 분해 및 시각화 실습
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.linalg import lu# 1. 행렬 A 설정
A = np.array([[2,3,1],
[4,7,3],
[-2,3,4]])
print("Matrix A:\n",A)
# 2. LU 분해 수행
# P : Permutation , L : Lower Triangular , U : Upper Triangular
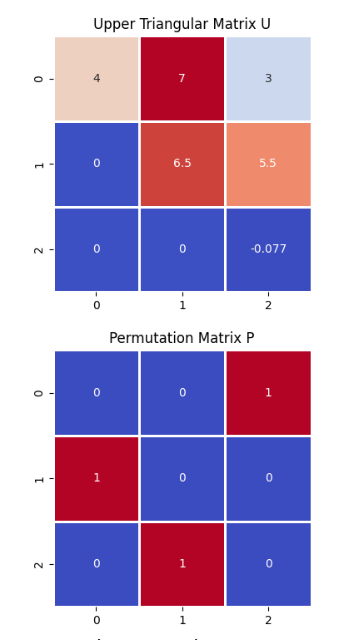
P, L ,U = lu(A)
print("\nLower Triangular Matrix L:\n",L)
print("\nUpper Triangular Matrix L:\n",U)
print("\nPermutation Matrix L:\n",P)
# 3. 행렬 시각화 함수
def plot_matrix(matrix,title):
plt.figure(figsize=(4,4))
sns.heatmap(matrix, annot=True,cmap='coolwarm',cbar=False,linewidths=1)
plt.title(title)
plt.show()
# 4. LU 분해 및 P 행렬 시각화
plot_matrix(A,"Matrix A")
plot_matrix(L,"Lower Triangular Matrix L")
plot_matrix(U,"Upper Triangular Matrix U")
plot_matrix(P,"Permutation Matrix P")
# 5. LU 분해 활용 예제
b = np.array([5,9,4])
# Ly = pb 풀이
y = np.linalg.solve(L,P@b)
# Ux = y 풀이
x = np.linalg.solve(U,y)
print("\nSolution x:",x)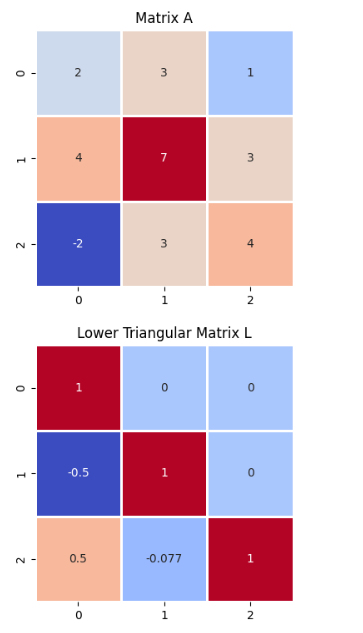
# 행렬식 계산
# det(A) = det(U)
det_A = np.linalg.det(U)
print("\ndet(A)=",det_A)
# 역행렬 계산
A_inv = np.linalg.inv(U) @ np.linalg.inv(L)
print("\nInverse of A:\n",A_inv)
'MIT 18.06 Linear Algebra' 카테고리의 다른 글
| 6.Column_Space_and_Nullspace (1) | 2025.04.01 |
|---|---|
| 5.Transposes,_Permutations,_Spaces_R^n (0) | 2025.04.01 |
| 3. Multiplication_and_Inverse_Matrices (0) | 2025.04.01 |
| Lecture 2. Elimination with Matrices (0) | 2025.03.02 |
| Lecture 1.2 The geometry of linear equations (0) | 2025.03.02 |